ابتدا لازم است که مقداری با فضای K آشنا شویم.
فضای K چیست؟ فضای k بخشی از حافظه سخت افزاری پردازشگر سیستم MRI می باشد که آرایه ای از نقطه داده یا data point هاست که حاوی اطلاعاتی از سیگنال دریافت شده از FOV مورد نظر ماست. در واقع اطلاعات تصویر در فضای k به صورت فرکانس های فضایی ذخیره می شوند که با استفاده از یک عملیات پیچیده ریاضی به نام تبدیل فوریه به تصویر مورد نظر ما تبدیل می شود.
فضای k دارای دو محور kx و ky می باشد که kx به صورت افقی و ky به صورت عمودی قرار گرفته است. بدین ترتیب هر نقطه داده روی فضای k دارای مختصات (kx,ky) می باشد که نمایانگر فاز و فرکانس آن دیتاپوینت است.
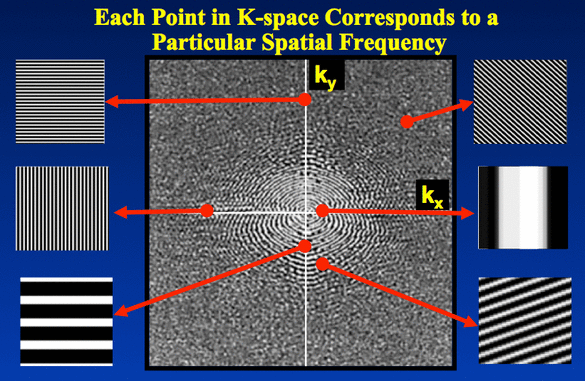
در مورد نحوه پر شدن فضای k به طور خلاصه در عموم سکانس های پالسی ابتدا یک پالس RF به اسلایس مورد نظر فرستاده می شود و آن مقطع را تهییج می کند و سیگنالی توسط کویل دریافت کننده دریافت می شود. هر یک سیگنال می تواند برای ما یک تصویر از آن مقطع ایجاد کند ولی ما برای اینکه به درستی عملیات کدگذاری فاز و فرکانس را انجام دهیم نیاز داریم که تعداد مشخصی از سیگنالها را داشته باشیم و آنها را درخطوط مختلف فضای K ذخیره کنیم.
برای مثال ما میخواهیم یک تصویر با ماتریس ۲۵۶*۲۵۶ داشته باشیم. در ماتریس تصویری عدد اول عدد فرکانس و عدد دوم عدد فاز می باشد. برای اینکار به طور ساده لازم است با کمک گرادیان کدگذاری فرکانس ۲۵۶ نمونه فرکانسی از سیگنال دریافتی برداریم و همچنین ۲۵۶ سیگنال با ۲۵۶ فاز مختلف که هر کدام با یک گرادیان کدگذاری فاز مختلف ایجاد شده اند در طی ۲۵۶= TR (البته نه در تمام سکانس های پالسی) داشته باشیم نمونه های حاصل از هر سیگنال را در یک خط از فضای k بریزیم. با این کار در واقع ما ۲۵۶*۲۵۶ عدد دیتاپوینت ایجاد کردیم که هر کدام دارای فاز و فرکانس مختص خود هستند و می توان از آن برای ساخت یک تصویر با ابعاد ۲۵۶*۲۵۶ پیکسل استفاده کرد.
حال از نظر مکان یابی و کدگذاری فاز و فرکانس مسئله حل شد. اما برای اینکه بدانیم هر پیکسل در تصویر دارای چه شدت سیگنالی خواهد بود باید مقدار شدت سیگنال را برای هر پیکسل در تصویری که قرار است نمایش داده شود مشخص کنیم. برای اینکار ما هنگامی که نمونه برداری میکنیم در واقع در جهت افقی یا kx بین نمونه های برداشته شده و مقدار بزرگی شدت سیگنال در هر سطر تمایز ایجاد میکنیم اما نمونه های برداشته شده از هر سیگنال حاصل از برایندشدت سیگنال ناشی از پروتون های موجود در تمامی آن ستون تصویری است. برای تعیین کردن شدت سیگنال بین پیکسل های هر ستون نیاز به تعدادی سیگنال با گرادیان کدگذاری فاز مختلف داریم تا از آنها برای حل معادلات و یافتن میزلان بزرگی شدت سیگنال برای هر پیکسل در یک ستون استفاده کنیم. برای روشن شدن مسئله موضوع را با یک مثال مطرح می کنیم
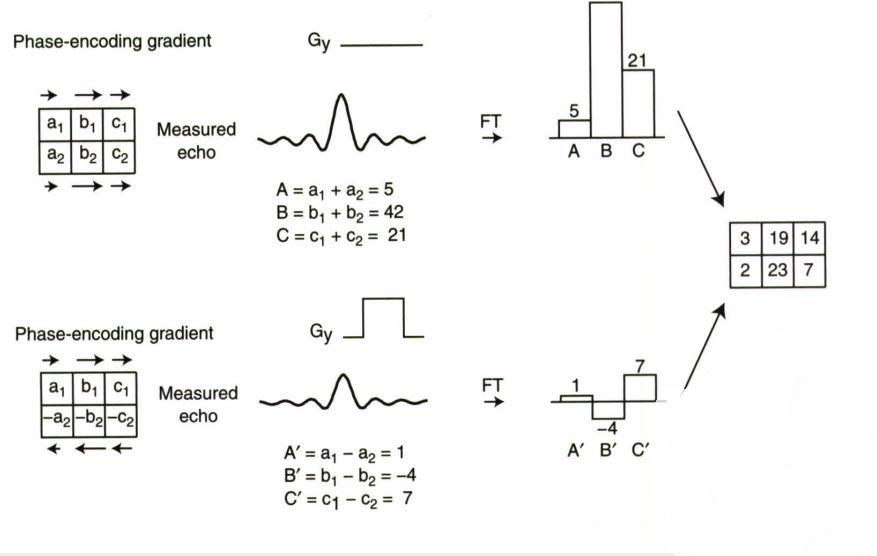
فرض کنید میخواهیم یک تصویر با ابعاد ۳*۲ بسازیم.تصویر ما دارای ۲ سطر و ۳ ستون و ۶ پیکسل خواهد بود. برای اینکار نیاز داریم که دو سیگنال با گرادیان کدگذاری فاز مختلف داشته باشیم. و همچنین از سیگنال مورد نظر ۳ نمونه فرکانسی داشته باشیم. طبق تصویر که زیر این مطلب قرار خواهد گرفت ما اولین سیگنال را بدون اعمال گرادیان کدگذاری فاز و دومین سیگنال را با اعمال گرادیانی که بین دو پیکسل مجاور در یک ستون ۱۸۰ درجه اختلاف فاز ایجاد میکند میگیریم. و از هر دو سیگنال ۳ نمونه فرکانسی میگیریم. طبق تصویر ما پیکسل های تصویر را در سطر بالا از چپ به راست با a1,b1,c1 و پیکسل های سطر دوم را با a2,b2,c2 نشان می دهیم.
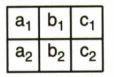
نمونه های برداشته شده از سیگنال اول بدون اعمال گرادیان کدگذاری فاز را با A,B,C نشان می دهیم که به ترتیب هر کدام مقدار شدت سیگنال برایند از ستون اول (a1+a2) ستون دوم (b1+b2) و ستون سوم (c1+c2) می باشند و مقدار عددی شدت سیگنال حاصل از این نمونه ها نیز به ترتیب A=5 B=42 C=21 می باشد.
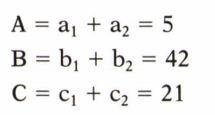
نمونه های برداشته شده از سیگنال دوم با اعمال گرادیان کدگذاری فاز را با A’,B’,C’, نشان می دهیم که به ترتیب هر کدام مقدار شدت سیگنال برایند از ستون اول (a1+a2) ستون دوم (b1+b2) و ستون سوم (c1+c2) می باشند و مقدار عددی شدت سیگنال حاصل از این نمونه ها نیز به ترتیب A’=5 B’=42 C’=21 می باشد.
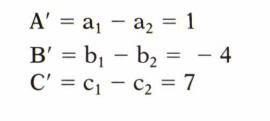
حال میبینیم که در هر ستون دو مقدار مجهول داریم یعنی a1 , a2 و همچنین دو معادله داریم یعنی a1+a2=5 و a1-a2=1 می توان با استفاده از جبر به راحتی مقدار a1 , a2 را حساب کنیم که a1=3 و a2=2 میشود. در مورد اینکه چرا با اعمال گرادیان کدگذاری فاز a1-a2 شد چون شدت سیگنال در هر ستون برایند شدت سیگنال پیکسل های آن ستون است و در حالتی که گرادیان کدگذاری فاز اعمال نشود نا همفازی بین پروتون های دو پیکسل ایجاد نمی شود و شدت سیگنال آنها با هم جمع می شود در صورتی که با اعمال گرادیان بین دو پیکسل مجاور ۱۸۰ درجه اختلاف فاز ایجاد میشود و سیگنا برایند دو پیکسل از هم کم می شود. حال با استفاده از همین روش می توان میزان شدت سیگنال b1 و b2 وc1 و c2 را نیز محاسبه نمود و تصویر مورد نظر را نمایش داد. برای ساخت تصویر با سایز بزرگتر نیز همین اصول حاکم است ولی با تعداد مجهول و معادلات بیشتر.
یکی دیگر از مفاهیمی که برای درک تصویربرداری موازی لازمه بدونیم آرتیفکت تاشدگی یا aliasing یا wraparound هست.
برای فهم این آرتیفکت ابتدا باید با تئوری نایکوئیست آشنا بشویم. این تئوری به ما میگوید که برای اینکه ما بتوانیم یک سیگنال با فرکانس مشخص (f) را با دقت کافی نمونه برداری کنیم که نمونه حاصل شکل سیگنال را به درستی نمایش دهد باید فرکانس نمونه برداری ما دوبرابر ماکزیمم فرکانس سیگنال ما باشد یعنی فرکانس نمونه برداری باید (۲f) باشد. به شکل زیر دقت کنید.
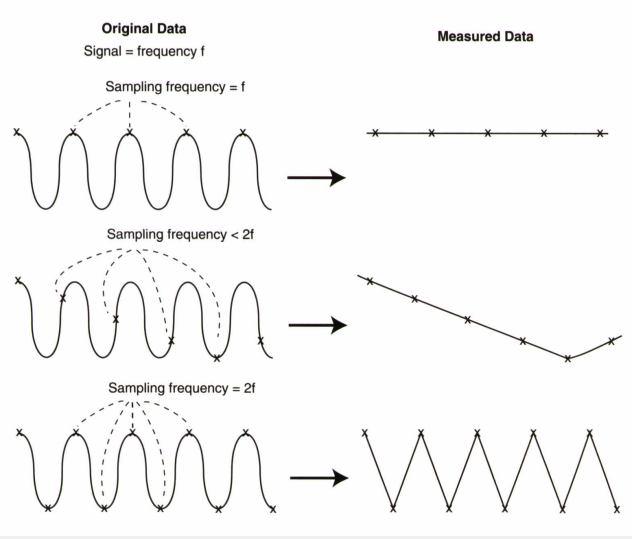
حال اگر میزان نمونه برداری ما کمتر از این حد باشد آرتیفکت تاشدگی رخ می دهد.. معمولا وقتی نمونه برداری ما کمتر از حد مجاز باشد ما مجبوریم FOV خود را محدود کنیم تا رزولوشن فضایی حفظ شود یا عکس این مورد که وقتی FOV کوچک انتخاب میکنیم در اصل میزان پهنای باند دریافتی خود که همان میزان نمونه برداری ما می باشد را کوتاه در نظر گرفته ایم.
برای درک این مطلب نیز به مثال زیر توجه کنید
در مقطع زیر که یک مقطع آگزیال در محدوده قلب می باشد FOV را کوچک در نظر گرفته ایم و بازو ها خارج از FOV قرار گرفته اند. پهنای باند دریافتی ما در این مثال مثبت و منفی ۱۶ کیلوهرتز می باشد. تئوری نایکوئیست حداقل فرکانس نمونه برداری برای این سیگنال را ۳۲ کیلوهرتز تعیین میکند. حال پروتون هایی که خارج از FOV قرار دارند اگرچه دلخواه ما نیست ولی در دو انتهای گرادیان کدگذاری فرکانس قرار دارند و در سیگنال دریافتی شرکت میکنند و در مولفه های high frequency قرار میگیرند.
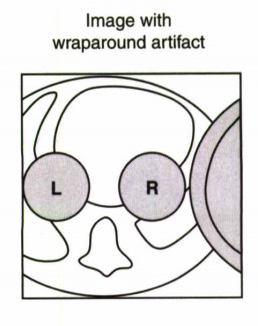
در مثال ما بافت بازوی راست با فرکانس ۲۴khz- و بازوی چپ با فرکانس ۲۰khz+ در حال چرخش می باشند. به دلیل پایین بودن فرکانس نمونه برداری ما این دو فرکانس به اشتباه به عنوان به ترتیب فرکانس های ۸khz+ و ۱۲khz- محسوب می شوند و سیگنال ناشی از بازوی چپ در سمت راست FOV و سیگنال ناشی از بازوی راست در سمت چپ FOV نمایش داده می شوند. مطابق شکل زیر
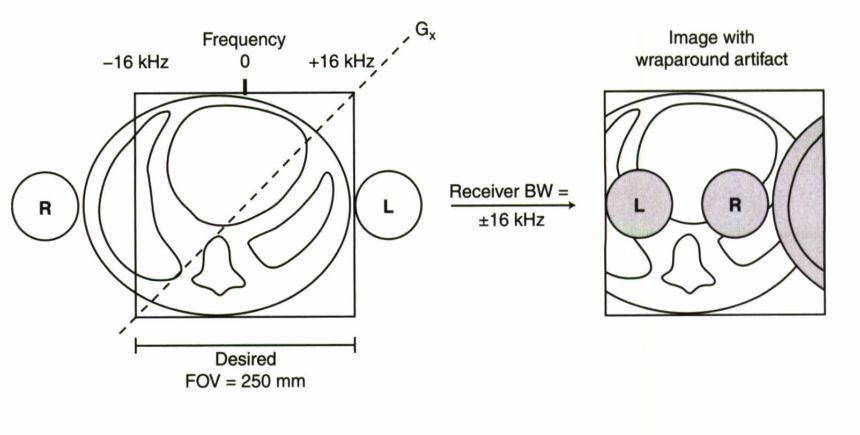
این آرتیفکت هم در جهت فاز و هم در جهت فرکانس ممکن است دیده شود. راهکارهایی برای رفع آن موجود است که از آن جمله : افزایش FOV و افزایش نمونه برداری در هر دو جهت می باشد که افزایش FOV به بهای کاهش رزولوشن فضایی می باشد و نمونه برداری بیش از حد در جهت فاز نیز می تواند به بالا رفتن زمان اسکن بیانجامد. البته به طور روتین در سکانس های امروزی نمونه برداری بیش از حد در جهت فرکانس به نحوی که تاشدگی رخ ندهد انجام می شود.چون روی زمان اسکن تاثیری ندارد.
حال با این مقدمات سراغ بحث اصلی یعنی تصویربرداری موازی می رویم.
تصویربرداری موازی روشی است که نیازمند کویل های خاصی به نام کویل های آرایه فازی می باشد. این نوع کویل ها به جای یک کویل دریافت کننده از ترکیبی از جند کویل ساخته شده که در یک یا چند ردیف کنار یکدیگر قرار گرفته اند.و هر کدام نسبت به ناحیه ای که در فاصله نزدیکتری نسبت به آن کویل قرار گرفته است حساسیت بیشتری دارد و از آنجا سیگنال بیشتری دریافت میکند. در نتیجه برای قسمت مشخصی از FOV ما هر کویل که نزدیکتر به آن ناحیه باشد حساسیت بیشتر و هر کویل دورتر از آن ناحیه باشد حساسیت کمتری خواهد داشت.
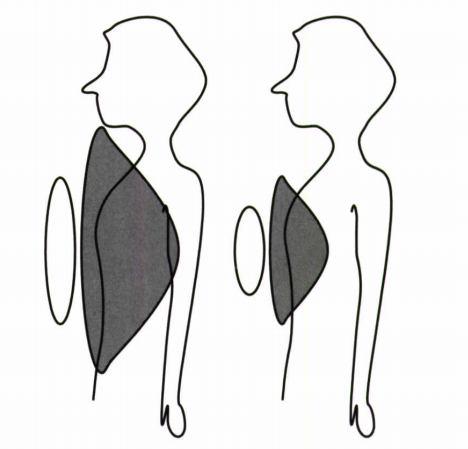
ضمنا اندازه هر کویل نیز میزان حساسیت به یک نقطه خاص را تعیین می کند
هر کویل آرایه فازی تعداد مساوی یا کوچکتر از تعداد کویل ها ، کانال دارد. تعداد این کانال ها می تواند ماکزیمم R فاکتور ما را تعیین کند و نه تعداد خود کویل ها.ما با استفاده از این کویل ها می توانیم مثلا برای یک تصویر با سایز ماتریس ۵۱۲*۵۱۲ با استفاده از این روش وفاکتور R=2 به جای ۵۱۲ مرحله کدگذاری فاز ۲۵۶ مرحله داشته باشیم و زمان اسکن نصف می شود و با فاکتور r=4 این زمان را به ۱/۴ برسانیم و ۱۲۸ خط را پر کنیم. بقیه خطوط توسط روش های خاصی که متعاقبا معرفی می شود پر می شوند.
فاکتور R نشان می دهد که undersampling فضای K با چه ضریبی انجام می شود و به تعداد چنل های دریافتی کویل بستگی دارد. البته افزایش بیش از حد R فاکتور نیز مشکل ساز است و SNR را به نحوی که بیان خواهد شد کاهش می دهد.
حال انواع روش های تصویربرداری موازی را با هم مرور می کنیم. این نوع تصویربرداری به دو روش به نام های SENSE و SMASH انجام میشود. تفاوت این دو روش در این است که SENSE در حوزه تصویر مشکل تا شدگی ناشی از UNDERSAMPLING را حل می کند ولی SMASH در حوزه فضای K این UNDERSAMPLING را جبران کرده و خطوط فضای K پر نشده را پر میکند.
واژه SENSE مخفف SENSitivity Encoding و واژه SMASH مخفف SiMultaneous Acquisition of Spatial Harmonics می باشد که در دستگاه های مختلف نام های متفاوتی دارد به عنوان مثال mSENSE در زیمنس و ASSET در GE و SENSE در فیلیپس و RAPID در هیتاچی و SPEEDER در توشیبا مورد استفاده قرار می گیرند در حالی که SMASH در زیمنس با نام GRAPPA و در GE با نام ARC شناخته میشود.
حال به معرفی اساس روش SENSE می پردازیم : در این روش ما با استفاده از کویل آرایه فازی سیگنال گرفته ایم و تصویر را ساخته ایم. تصویر به دلیل UNDERSAMPLING در جهت کدگذاری فاز دارای آرتیفکت تا شدگی می باشد. در روش SENSE ما با استفاده از مقدار سیگنال دریافتی توسط هر کویل و در دسترس داشتن مقدار حساسیت آن کویل به نقطه مورد نظر که در یک پیکسل تصویر قرار گرفته است تا شدگی را از آن پیکسل رفع کنیم. ما برای مثال آن پیکسل مورد نظر را مانند شکل زیر در ناحیه تا شده انتخاب می کنیم :
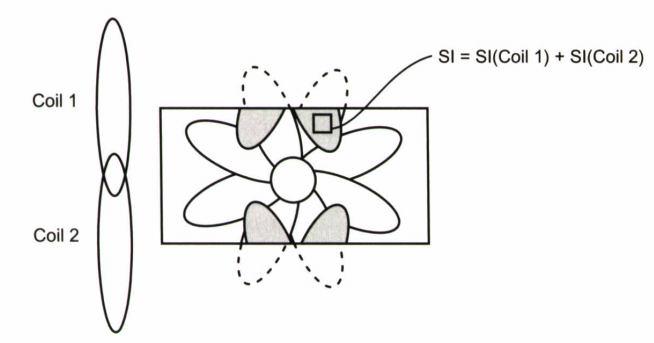
همان طور که مشاهده می شود در پیکسل مورد نظر شدت سیگنال ناشی از دو ناحیه است. یکی ناحیه ای که مربوط به تصویر واقعی نیست و به ناحیه ای بیرون از fov در طرف دیگر تصویر مربوط است که تا شده و در آنجا قرار گرفته و دیگری ناحیه ای که واقعا مربوط به همان پیکسل می شود. حال ما باید تشخیص بدهیم چه مقدار از شدت سیگنال آن پیکسل مربوط به ناحیه تا شده است و آن مقدار را از شدت سیگنال کلی کم میکنیم تا تاشدگی برطرف شود.
برای اینکار نیاز داریم تا برای پیکسل مورد نظر مقدار شدت سیگنال اندازه گیری شده توسط هر کویل به صورت جداگانه و همچنین میزان حساسیت هر کویل به ناحیه مورد نظر را داشته باشیم که حساسیت کویل توسط خود سیستم قبل از اجرای سکانس اندازه گیری می شود.
حال به طور مثال، در تصویر ناحیه مشخص شده با مربع نسبت به کویل ۱ نزدیکتر است و کویل ۱ حساسیت بیشتری به آن ناحیه دارد و سیگنال بیشتری نسبت به کویل ۲ از آن ناحیه میگیرد. ولی در عوض کویل شماره ۱ نسبت به ناحیه تا شده که در پایین تصویر قرار دارد حساسیت کمتری نسبت به کویل ۲ دارد.حال طبق شکل زیر شدت سیگنال واقعی مربوط به پیکسل را با نماد زیر نشان می دهیم :
![]()
و شدت سیگنال ناحیه تا شده در ناحیه مورد نظر را با نماد زیر نشان می دهیم :
![]()
حال برای شدت سیگنال بدست آمده توسط هر کویل می توان معادلات زیر را نوشت و توسط دو معادله به دست آمده دو مجهول که با شکل های بالا مشخص می شدند را به دست آورد و شدت سیگنال واقعی را درون پیکسل قرار داد و تا شدگی را رفع کرد .

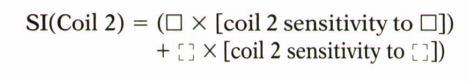
برای درک بهتر مسئله یک مثال ذکر میکنیم. فرض کنیم در پیکسل مشخص شده در تصویر فوق حساسیت کویل ۱ به ناحیه مورد نظر ۰٫۹ و به ناحیه تا شده ۰٫۲ و حساسیت کویل دو به ناحیه مورد نظر ۰٫۱ و به ناحیه تا شده ۰٫۸ باشد. و شدت سیگنال دریافتی کلی توسط کویل ۱ برابر با ۳۷ و توسط کویل ۲ برابر با ۴۳ باشد. با عدد گذاری در فرمول های بالا دو معادله و دو مجهول به دست می آید که مقدار واقعی شدت سیگنال ناحیه مورد نظر که مربه شکل است را می یابیم و درون پیکسل می گذاریم تا تا شدگی برطرف شود

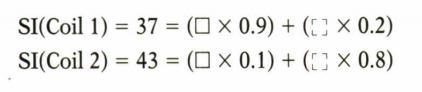
که در مثال ما این مقدار عدد ۳۰ بدست می آید.
حال برای فاکتور های بیش از ۲ نیز اصول همین است فقط برای R=4 به عنوان مثال ۴ معادله و ۴ مجهول خواهیم داشت.
شکل شماتیک برای SENSE :
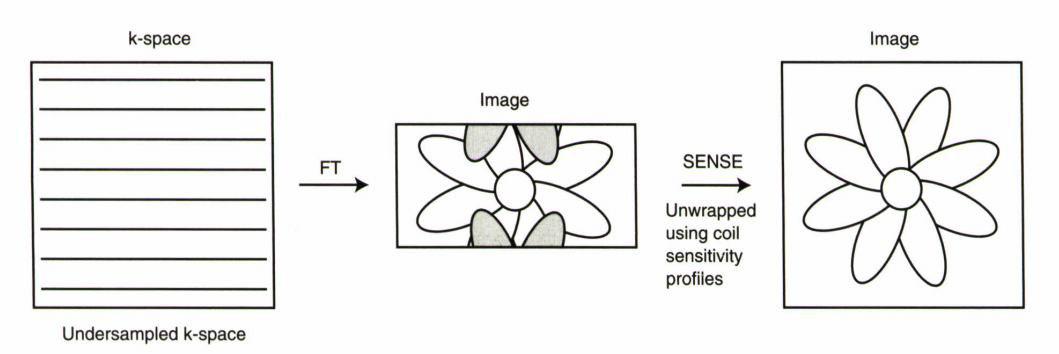
و اما روش SMASH :
در این روش قرار است قبل از ساخت تصویر و در فضای k ، این undersampling به وجود آمده را جبران کنیم. برای مثال :
اولین اکو توسط گرادیان کدگذاری فاز صفر جمع آوری شده و در خط مرکزی فضای k ریخته می شود.و اکوی دوم را جمع آوری نمیکنیم و سراغ اکوی سوم می رویم . اما اکوی دوم را با محاسبات پر خواهیم کرد. محاسبه آن نیز به صورت تصاویر زیر است:

طبق تصویر بالا خط اول فضای K توسط دیتای واقعی جمع آوری شده از تصویر پر می شود ولی خط دوم دیتای بازسازی شده توسط مقدار سیگنال اندازه گیری شده از کویل های مختلف پر می شود.
حال اگر بخواهیم با فاکتور R=3 تصویربرداری موازی انجام دهیم از هر ۳ مرحله کدگذاری فاز ۱ مرحله را واقعا دیتا میگیریم و دو مرحله بعدی را دیتای بازسازی شده توسط فرمول زیر بدست می آوریم و دو خط را پر می کنیم :
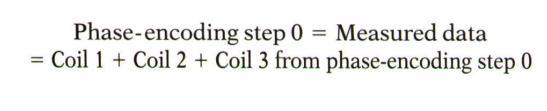

شکل شماتیک روش SMASH:
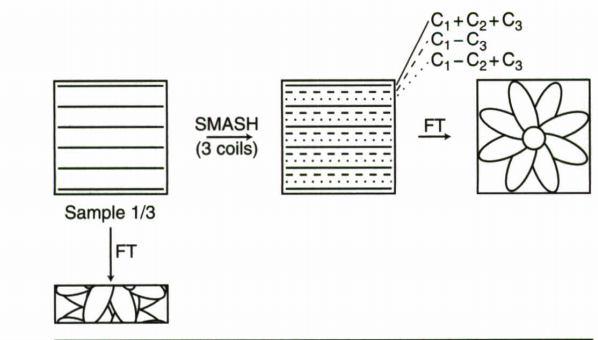
حال قسمت پایانی بحث را مطرح می کنیم
جالش های موجود در تصویربرداری موازی:
۱٫دقت اندازه گیری حساسیت کویل ها توسط دستگاه بسیار مهم و تاثیر گذار است و به دلایلی مثلا حرکت بیمار در حین اندازه گیری پروفایل حساسیت ممکن است اشتباه شود. پس از اندازه گیری حساسیت کویل یک SENSITIVITY MAP به دست می آید.
۲٫چالش دیگر نیاز به محاسبات سریع و پیچیده توسط دستگاه و چک کردن صحت عملکرد الگوریتم های پردازشی است.
۳٫چالش بعدی کاهش SNR می باشد که یکی از عدم مزایای مهم در این روش تصویربرداری محسوب می شود که به دلیل UNDERSAMPLING فضای K به وجود می آید و طبق فرمول زیر وابستگی معکوس به ریشه دوم فاکتور R و g دارد
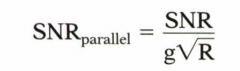
فاکتور g وابستگی مکانی پروفایل حساسیت به یک نقطه خاص است که در طول fov ثابت نیست و به همین دلیل SNR در جاهای مختلف FOV متغیر است
ولی با وجود تمامی این عدم مزایا کاهش دراماتیک زمان اسکن با حفظ قدرت تفکیک فضایی بسیار وسوسه انگیز و در آن واحد بسیار کاربردی می باشد و استفاده از این نوع تصویربرداری را در برخی کاربردها اجتناب ناپذیر جلوه می دهد.
مقایسه ای بین دو روش SENSE و SMASH و کاربرد هر کدام: ۱-روش SMASH کمی طولانی تر از روش SENSE می باشد به دلیل زمان اضافی که صرف self-calibration خطوط فضای k می شود. ۲- روش SENSE کمی SNR بیشتر نسبت به GRAPPA دارد مخصوصا در R فاکتور های بالاتر. ۳-در جاهایی مثل قفسه صدری که ناحیه ای غیریکنواخت می باشد SENSE ضعیف تر عمل می کند.چون پروفایل حساسیت کویل به درستی اندازه گیری نمی شود. ۴- SENSE در برابر آرتیفکت حرکتی آسیب پذیر تر است علی الخصوص اگر بین دو مرحله ی کالیبراسیون و تصویر گیری باشد. ۵- GRAPPA در FOV های کوچک تر بهینه تر عمل می کند . اما SENSE در FOV کوچک در جهت کدگذاری فاز مستعد آرتیفکت تا شدگی می باشد. ۶- GRAPPA در تصویربرداری های EPI SINGLE SHOT بهینه تر می باشد چون DISTORTION ناشی از SUSSEPTIBILITY کمتر روی تصویر اثر می گذارد.
برای این سوال که استفاده از روش های تصویربرداری موازی همواره توصیه می شود یا خیر جواب مشخصی وجود ندارد. اگر بتوان توسط سایر روش ها به قدرت تفکیک فضایی و زمانی مورد نظر خود رسید استفاده از این روش توصیه نمی شود ولی جایی که نیازمند این قدرت تفکیک ها باشیم استفاده از روش های تصویربرداری موازی بسیار سودمند خواهد بود.
ضمنا به یاد داشته باشیم تصویربرداری موازی یک سکانس پالسی نیست. بلکه یک تکنیک بازسازی تصاویر است. و آپشنی است که می توان به هر سکانس پالسی (SE, GRE, DWI, IR, MRA, etc) اضافه کرد و سرعت آن سکانس پالسی را بالاتر برد.
منبع: گروه تلگرام Optimizing MRI Sequences
تهیه کننده : آقای حسین جمله




