همانطور که می دانید مرکز فضای K شامل اطلاعات درباره ی پایین ترین فرکانس های فضایی و حاشیه ی این فضا شامل بالاترین فرکانس های فضایی است.
اما مهم است بدانیم که مرکز فضای K نشان دهنده ی محتوای تصویر در مرکز تصویر نیست.
فرکانس های فضایی پایین موجود در مرکز فضای K منعکس کننده ی سایه های سفید و خاکستری و مشکی موجود در تصویر هستند. اگر به طور کلی تصویر روشن باشد و یا شدت سیگنال بالا که با رنگ سفید در تصویر دیده می شوند داشته باشد، مرکز فضای K نیز روشن تر خواهد بود.
همچنین فرکانس های بالای موجود در حاشیه ی فضای K مربوط به دید جزئیات هستند. به عنوان مثال دیدن لبه های ساختارهای ریز با قدرت تفکیک فضایی بالا مستلزم وجود این فرکانس های بالا در سیگنال دریافتی ذخیره شده در فضای K است.
برای درک مطالب بالا به شکل زیر توجه نمایید .

در شکل بالا سهم هر قسمت از فضای K در تشکیل تصویر برشی از قلب را ملاحظه می نمائید. در ردیف اول از کل اطلاعات موجود در فضای K شامل فرکانس های بالا و پایین استفاده شده است و تصویر به دست آمده است. در ردیف دوم در شکل سمت چپ از ۱% از اطلاعات فضای K که در قسمت مرکزی واقع شده تصویر تشکیل شده و در شکل سمت راست، تصویر از ۹۹ درصد مابقی فضای K شکل گرفته است. در ردیف بعدی در سمت چپ ۴ درصد مرکزی و سمت راست ۹۶ درصد و ردیف بعدی سمت چپ ۱۵ درصد و سمت راست ۸۵ درصد مابقی در تشکیل تصویر سهم دارند.
با نگاهی به تصاویر تشکیل شده از هر فضای K در سمت راست این امر اثبات می شود که استفاده از اطلاعات حاشیه ی فضای K دیدن لبه های موجود در ساختارهای تصویر را میسر می سازد و ملاحظه ی تصاویر سمت چپ نیز نشان می دهد اطلاعات مرکز فضای K کنتراست کلی تصویر و سیاهی و سفیدی موجود را نشان می دهد.
فضای K دارای مولفه های حقیقی و موهومی از سیگنال دریافتی است که تصویر بدست آمده در MRI معمولا از تبدیل فوریه ی ترکیبی از این مولفه هاست و تصویر مگنتیود نام دارد، اگرچه می توان تصویر حقیقی یا موهومی نیز به صورت جدا به دست آورد. همچنین علاوه بر بازسازی مگنتیود، بازسازی فاز نیز برای ساخت تصویر وجود دارد که کاربرد خاص خود را داشته و نسبتا کمتر در MRI مورد استفاده قرار می گیرد.
هر قسمت از سیگنال دریافتی و ذخیره شده در فضای K که حاصل نمونه برداری از سیگنال القا شده در کویل است اهمیت خاص خود را دارد و نقش اساسی در کیفیت تصویر ایفا می کند. به همین دلیل باید از تمامی اطلاعات موجود در فضای K برای ساخت تصویر استفاده کنیم و در صورت حذف قسمتی از آن یا نمونه برداری کمتر از حد دچار آرتیفکت هایی از قبیل ترانکیشن و تاشدگی و … می شودیم. برای روشن شدن این موضوع به مثال زیر توجه کنیم:
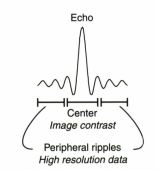
در سیگنال تصویر بالا قسمت های با فرکانس پایین در مرکز و فرکانس بالا در حاشیه ی سیگنال مشخص شده اند که در ناحیه ی مربوط به خود در فضای K قرار می گیرند. حال برای مثال اگر ما کمتر از نمونه برداری کنیم و قسمت حاشیه ای سیگنال را که شاید در نگاه اول کم اهمیت به نظر برسد حذف کنیم چه اتفاقی برای تصویر مربوط می افتد؟ برای یافتن پاسخ به تصویر زیر نگاه کنیم:
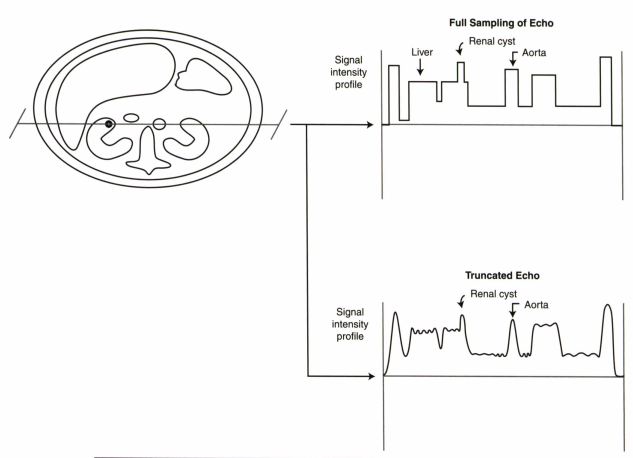
در صورتی که اطلاعات ناحیه ی حاشیه ای سیگنال را بیش از حد نمونه برداری کنیم پروفایل شدت سیگنال مربوط به تصویر مثل شکل بالا خواهد بود که لبه ی ساختار ها کاملا مجزا خواهند بود و همین امر باعث بالا رفتن قدرت تفکیک فضایی تصویر می شود، ولی در صورتی که قسمت های حاشیه ای کمتر نمونه برداری شوند پروفایل شدت سیگنال در تصویر به صورت شکل پایینی بوده و لبه ی ساختار ها کاملا از هم قابل تشخیص نخواهد بود.
ابعاد فضای K و فضای بین دیتا پوینت ها و ارتباط با تصویر:
مشابه تصویر MRI، خود فضای K نیز ابعاد قابل اندازه گیری و سایز کلی معنی داری دارد.
آرایه ی مقادیری که فضای K را شکل می دهند می تواند به عنوان یک تصویر با ابعاد معین به نام دلتا کا در نظر گرفته شود که در سه جهت X ,Y , Z وجود دارد.دلتا کا در هر جهت دارای مقدار برابر با فاصله ی بین دیتاپوینت ها در آن جهت است. اندازه ی کا ی کلی در هر جهت از جمع بین تمامی دلتا کا ها در یک جهت به دست می آید. تعداد دلتا کا برابر با سایز ماتریس در آن جهت خواهد بود.
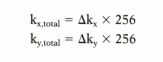
هرچقدر یک دیتا پوینت در دلتا کای دورتری از مرکز قرار داشته باشد دارای فرکانس فضایی بالاتری است و در نتیجه در صورت داشتن یک فضای K بزرگ نسبت به یک فضای K کوچک فرکانس فضایی بالاتر بوده و قدرت تفکیک فضایی افزایش خواهد یافت. نکته ی مهم این است که ابعاد فضای K به صورت معکوس با سایز وکسل تصویر در ارتباط است و ابعاد تصویر به صورت معکوس به وکسل سایز فضای K یعنی دلتا کا ربط دارند. برای مثال در تصویر زیر تصویر A و C هر دو میدان دید یکسانی دارند و دلتا کا ی این دو تصویر در فضای K ی مربوط به خود یکسان است. ولی چون مقدار کای کلی یا توتال در جهت X و Y شان با هم متفاوت است، قدرت تفکیک فضایی متفاوت دارند. همچنین دو تصویر B و C هر دو دارای رزولوشن فضایی یکسان هستند و قدرت تفکیک فضایی یکسان دارند، ولی چون اندازه ی کلی فضای K در شکل B کوچکتر است، میدان دید در تصویر شکل B بزرگتر است و رابطه ی معکوس دارند.
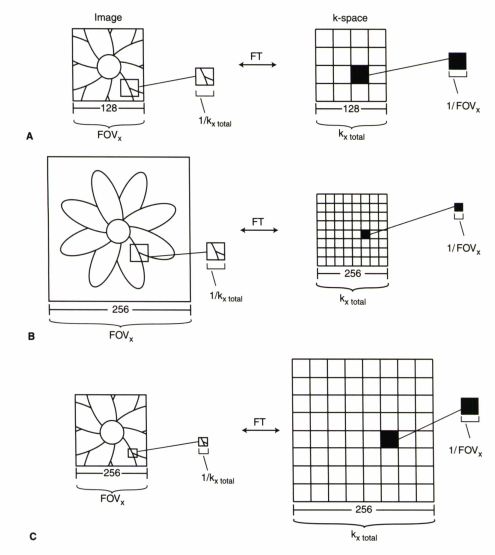
سایز ماتریس تصویر معمولا برابر با سایز ماتریس فضای K است برای مثال هر دو ۲۵۶*۲۵۶٫
دلتا کای فضای K به وسیله ی معادله ی زیر با میدان دید تصویر رابطه ی معکوس دارد. یعنی هرچقدر دلتا کا بیشتر شود، میدان دید کوچکتر می شود.
![]()
همچنین اندازه ی کلی فضای K نیز با قدرت تفکیک فضایی تصویر و سایز وکسل در تصویر مرتبط اند. یعنی برای بدست آوردن قدرت تفکیک فضایی بالاتر و سایز وکسل کوچکتر باید دلتا کا ی کلی فضای K افزایش دهیم
![]()
در صورت داشتن سوال در مورد این بحث در قسمت دیدگاه ها مطرح فرمایید.
منبع: CARDIOVASCULAR MRI
تهیه کننده: جناب آقای جمله




